Langkah-Langkah Activity Network Diagram Penjadwalan Proyek
Seperti dijelaskan pada bagian pertama dari tulisan tentangactivity network diagram ini, meskipun saat ini kebanyakan paket software manajemen proyek didasarkan pada diagram AON, tapi bukan berarti diagram AOA sudah punah. Bahkan untuk aktivitas brainstorming, diagram AOA sangat berguna saat perencanaan team di awal proyek karena diagram ini jauh lebih mudah digambarkan dengan sketsa tangan.
Pada bagian kedua ini akan diuraikan langkah-langkah membuat activity network diagram dari suatu proyek dengan tujuan untuk mengidentifikasi jalur kritis (critical path) dan mencari tahu berapa banyak waktu yang dihabiskan untuk menyelesaikan proyek. Metode yang digunakan adalah metode diagram AOA.
1. Membuat Daftar Kegiatan Proyek atau Proses
Analisis activity network diagram dimulai dengan menyiapkan dan menyusun daftar kegiatan atau pekerjaan yang diperlukan dalam rencana proyek atau proses. Untuk setiap kegiatan, kita perlu tahu apakah ada kegiatan lain yang harus dilakukan sebelum memulai kegiatan tersebut (predecessor) , dan berapa lama kegiatan tersebut harus dilakukan (durasi). Jangan lupa memberikan kode untuk setiap jenis kegiatan (misalnya dengan huruf: A, B, C, D, dan seterusnya) agar memudahkan saat menggambar dan menganalisis diagram. Tabel 1 berikut adalah contoh daftar kegiatan yang diperlukan dalam rencana suatu proyek.
Tabel 1
Daftar Kegiatan Proyek
| Kegiatan | Deskripsi | Predecessor Kegiatan | Durasi, bulan |
| A | Perancangan produk | — | 5 |
| B | Penelitian pasar | — | 1 |
| C | Analisis produksi | A | 2 |
| D | Model produk | A | 3 |
| E | Brosur penjualan | A | 2 |
| F | Analisis biaya | C | 3 |
| G | Pengujian produk | D | 4 |
| H | Pelatihan penjualan | B, E | 2 |
| I | Penetapan harga | H | 1 |
| J | Pelaporan proyek | F, G, I | 1 |
2. Menggambar Diagram
Metode analisis yang akan dipakai dalam contoh ini menggunakan diagram AOA sehingga setiap node merupakan tahap penyelesaian proyek. Simbol yang digunakan untuk node biasanya berupa lingkaran seperti yang diperlihatkan Gambar 1 di bawah ini.
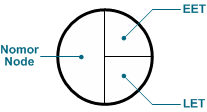
Gambar 1. Simbol Node
Agar dapat menyajikan informasi yang diperlukan, simbol node berbentuk lingkaran dibagi tiga ruang, ruang pertama sebelah kiri digunakan untuk memberi identitas peristiwa yang berupa nomor node. Ruang kedua dan ketiga sebelah kanan digunakan untuk memperlihatkan kapan terjadinya kejadian (peristiwa), yang mana bagian kanan atas menunjukkan waktu peristiwa paling awal atau earliest event time (EET) dan bagian kanan bawah menunjukkan waktu peristiwa paling akhir atau latest event time(LET).
Untuk menggambarkan setiap kegiatan yang ada dalam daftar kegiatan proyek, kita memulai dengan membuat node nomor 1. Dari node nomor 1, tarik keluar garis panah kegiatan yang tidak memiliki predecessor, yakni: A dan B. Jangan lupa bubuhkan kode kegiatan pada pangkal garis panah diikuti oleh durasinya. Kemudian, buat node nomor 2 di ujung garis panah A, dan nodenomor 3 di ujung garis panah B.
Oleh karena A adalah predecessor bagi C, D, dan E maka tarik keluar garis panah untuk C, D, dan E dari node nomor 2. Buat node nomor 4 pada ujung garis panah C dan node nomor 5 pada ujung garis panah D. Sedangkan untuk garis panah E tidak dibuatkan node baru melainkan masuk ke nodenomor 3 (node di ujung garis panah B). Hal ini karena B dan E sama-sama menjadi predecessor untuk H saja.
Buatlah garis panah dan node berikutnya sampai semua kegiatan tergambarkan. Hasilnya akan terlihat seperti Gambar 2 di bawah ini.

Gambar 2. Konstruksi Activity Network Diagram
Beberapa konvensi tentang bagaimana cara menggambar diagram AOA adalah:
- Semua kegiatan tanpa predecessor datang dari node nomor 1.
- Semua kegiatan tanpa successor mengarah ke node nomor terbesar (node terakhir).
Dalam contoh yang diperlihatkan Gambar 2, A dan B adalah dua kegiatan yang tidak memiliki predecessor. Keduanya berbentuk garis panah yang keluar dari node nomor 1.
Lihat juga J adalah kegiatan yang tidak memiliki successor. Oleh karena itu, garis panah J masuk ke node terakhir, yaitu node nomor 8 (node nomor terbesar dalam contoh ini). Jika ada lebih dari satu kegiatan tanpa successor, maka semua garis panah kegiatan masuk ke node nomor terbesar.
3. Menghitung dan Menganalisis Earliest Event Time (EET)
Cara menentukan earliest event time (EET) pada setiap node adalah dengan menggunakan perhitungan ke muka (forward), yaitu: kita mengawali perhitungan dari node nomor 1 dengan anggapan waktu mulai sama dengan nol, selanjutnya bergerak dalam jaringan untuk menghitung:
● EET yang terjadi, Ei,
● waktu mulai tercepat atau earliest start (ES), dan
● waktu selesai tercepat atau earliest finish (EF)
untuk setiap kegiatan dalam jaringan sampai perhitungan berakhir di nodeterakhir. Berikut metode perhitungannya:
| (i) | Jadikan EET yang terjadi pada permulaan proyek sama dengan nol, artinya, | |
| E1 = 0. | ||
| (ii) | ES untuk setiap kegiatan (i,j) adalah sama dengan Ei untuk peristiwa sebelumnya, artinya, | |
| ESij = Ei. | ||
| (iii) | EF untuk setiap kegiatan (i,j) adalah sama dengan ES ditambah durasi kegiatan. Artinya, | |
| EFij = ESij + Dij, | ||
| atau | EFij = Ei + Dij. | |
| (iv) | EET untuk peristiwa j adalah maksimum EF dari semua kegiatan yang berakhir ke dalam peristiwa tersebut. Artinya, | |
Ej = maxi {EFij untuk semua predecessor (i,j)}
| ||
Ej = maxi {Ei + Dij}
| ||
| yang mana D adalah durasi kegiatan. Dalam perhitungan ini, kegiatan diidentifikasi oleh predecessor node (atau peristiwa) i dan successor node j. | ||
Untuk activity network diagram Gambar 2, perhitungan EET adalah sebagai berikut:
| Langkah 1 | → | E1 | = | 0 | |
| Langkah 2 | |||||
| j = 2 | → | E2 | = | max{E1 + D12} = max{0 + 5} = 5 | |
| j = 3 | → | E3 | = | max{E1 + D13; + E2 + D23} | |
| = | max{0 + 1; 5 + 2} = 7 | ||||
| j = 4 | → | E4 | = | max{E2 + D24} = max{5 + 2} = 7 | |
| j = 5 | → | E5 | = | max{E2 + D25} = max{5 + 3} = 8 | |
| j = 6 | → | E6 | = | max{E3 + D36} = max{7 + 2} = 9 | |
| j = 7 | → | E7 | = | max{E4 + D47; E5 + D57; E6 + D67} | |
| = | max{7 + 3; 8 + 4; 9 + 1} = 12 | ||||
| j = 8 | → | E8 | = | max{E7 + D78} = max{12 + 1} = 13 | |
Hasilnya akan terlihat seperti Gambar 3 di bawah ini.
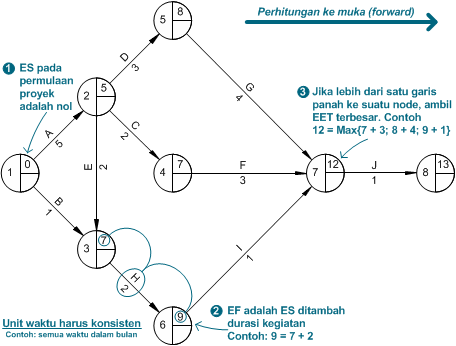
Gambar 3. Perhitungan ke Muka untuk Menghitung dan Menganalisis Earliest Event Time (EET)
Dengan demikian, waktu minimum yang diperlukan untuk menyelesaikan proyek ini adalah 13 bulan, E(8) = 13.
4. Menghitung dan Menganalisis Latest Event Time (LET)
Untuk menentukan latest event time (LET) pada setiap node adalah dengan menggunakan perhitungan ke belakang (backward), yaitu: perhitungan waktu mulai terlama atau latest start (LS) dan waktu selesai terlama atau latest finish (LF) untuk setiap kegiatan dalam jaringan yang dimulai dari nodeterakhir dengan Ln sama dengan En pada node terakhir (yang kita ketahui dari perhitungan ke muka) sampai perhitungan berakhir di node nomor 1. Berikut metode perhitungannya:
| (i) | Untuk peristiwa terakhir anggap | |
| En = Ln. | ||
| Ingat bahwa semua ES telah dihitung pada tahap perhitungan ke muka. | ||
| (ii) | LF untuk setiap kegiatan (i,j) adalah sama dengan LET dari peristiwaj, | |
| LFij = Lj. | ||
| (iii) | LS untuk setiap kegiatan (i,j) adalah sama dengan LF dikurangi durasi kegiatan. Artinya, | |
| atau, | LSij = LFij – Dij, | |
| atau | LSij = Lj – Dij. | |
| (iv) | LET untuk peristiwa i adalah minimum LS dari semua kegiatan yang berasal dari peristiwa tersebut. Artinya, | |
Li = minj {LSij untuk semua successor (i,j)}
| ||
Li = minj {LFij – Dij}
| ||
Li = minj {Lj – Dij}
| ||
Perhitungan LET untuk proyek dalam Tabel 1 adalah sebagai berikut:
| Langkah 1 | → | L8 | = | E8 = 13 | |
| Langkah 2 | |||||
| i = 7 | → | L7 | = | min{L8 – D78} = min{13 – 1} = 12 | |
| i = 6 | → | L6 | = | min{L7 – D67} = min{12 – 1} = 11 | |
| i = 5 | → | L5 | = | min{L7 – D57} = min{12 – 4} = 8 | |
| i = 4 | → | L4 | = | min{L7 – D47} = min{12 – 3} = 9 | |
| i = 3 | → | L3 | = | min{L6 – D36} = min{11 – 2} = 9 | |
| i = 2 | → | L2 | = | min{L3 – D23; L4 – D24; L5 – D25} | |
| = | min{9 – 2; 9 – 2; 8 – 3} = 5 | ||||
| i = 1 | → | L1 | = | min{L2 – D12; L3 – D13} | |
| = | min{5 – 5; 5 – 1} = 0 | ||||
Hasilnya akan terlihat seperti Gambar 4 di bawah ini.

Gambar 4. Perhitungan ke Belakang untuk Menghitung dan Menganalisis Latest Event Time (LET)
Bila kita perhatikan Gambar 4 di atas terdapat beberapa nodedengan EET = LET. Inilah node yang akan berada pada jalur kritis (critical path).
5. Menentukan Jalur Kritis
Definisi jalur kritis menurut salah satu penemu CPM adalah:
If there is a path from origin to terminus whose length equals the duration of the schedule, it is called a critical-path. (Kelley, 1961, p. 317)
Dengan kata lain total waktu jalur kritis akan sama dengan umur proyek. Hal ini berarti jalur kritis adalah jalur yang memiliki waktu terpanjang dari semua jalur yang dimulai dari peristiwa awal sampai peristiwa yang terakhir dalam activity network diagram.
Oleh karena itu, jalur kritis menunjukkan kegiatan-kegiatan kritis di dalam proyek. Kelley (1961) menambahkan tentang maksud kegiatan-kegiatan kritis:
All the activities in a critical-path are limiting in the sense that a delay in any one of them will cause a comparable delay in the completion of the project. Therefore, they are called critical activities. (Kelley, 1961, p. 317)
Maksudnya, suatu kegiatan disebut dengan kegiatan kritis bila suatu delay atau penundaan waktu di kegiatan ini akan mempengaruhi waktu penyelesaian keseluruhan dari proyek. Oleh karena itu, kegiatan disebut tidak kritis bila kegiatan ini mempunyai delay. Delay pada kegiatan tidak kritis disebut slackatau float time (waktu mengambang).
Konsep float sangat berharga karena memberikan fleksibilitas atau “ruang manuver” pada penjadwalan untuk menyelesaikan tugas-tugas tertentu sehingga ada suatu periode waktu di mana kegiatan dapat meleset tetapi tidak mempengaruhi jalur kritis dan tanggal penyelesaian. Menurut Hendrickson & Tung (2008), terdapat tiga kategori float, yaitu:
| (i) | Free float adalah banyaknya delay yang dapat ditugaskan untuk setiap satu kegiatan tanpa menunda kegiatan selanjutnya. Free float,FFij, untuk aktivitas (i,j) adalah: | |
| FFij = Ej – Ei – Dij. | ||
| (ii) | Independent float adalah banyaknya delay yang dapat ditugaskan untuk setiap satu kegiatan tanpa menunda kegiatan selanjutnya atau membatasi penjadwalan kegiatan sebelumnya. Independen float, IFij, untuk kegiatan (i,j) dihitung sebagai berikut: | |
IFij = {0Ej – Li – Dij
| ||
| (iii) | Total float adalah maksimum banyaknya delay yang dapat ditugaskan untuk setiap kegiatan tanpa menunda keseluruhan proyek.Total Float, TFij, untuk setiap kegiatan (i,j) dihitung sebagai berikut: | |
| TFij = Lj – Ei – Dij | ||
Secara grafis, ketiga macam float time dan slack time diilustrasikan pada contoh Gambar 5 berikut.
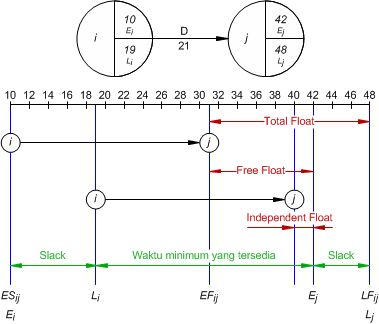
Gambar 5. Ilustrasi Contoh Float Time dan Slack Time
Delay kegiatan di jalur kritis akan menyebabkan delay waktu penyelesaian proyek, sedang delay di jalur tidak kritis mungkin tidak akan menunda waktu penyelesaian proyek sejauh delay tidak melebihi slack danfloat time untuk masing-masing kegiatan tidak kritis
Dalam suatu activity network diagram mungkin saja kita menemui lebih dari satu jalur kritis, bahkan semua jalur memungkinkan untuk menjadi jalur kritis. Jalur kritis memiliki kepekaan sangat tinggi atas keterlambatan penyelesaian suatu proyek. Keterlambatan pada jalur ini akan memperlambat penyelesaian waktu proyek secara keseluruhan, meskipun kegiatan lain tidak mengalami keterlambatan. Kita dapat mempercepat penyelesaian proyek secara keseluruhan dengan mempercepat waktu penyelesaian kegiatan kritis. Jalur kritis dapat saja berubah sebagai akibat dari keterlambatan atau percepatan penyelesaian kegiatan.
Cara menentukan jalur kritis pada activiy network diagram adalah dengan menulusuri jalur terpanjang dari awal sampai akhir proyek, yakni jalur yang melalui node dengan EET = LET, kemudian tandai jalur kritis tersebut dengan garis tebal atau berwarna. Perhatikan Gambar 6 di bawah ini, jalur yang ditandai dengan garis berwarna merah adalah jalur kritis untuk proyek dalam Tabel 1.
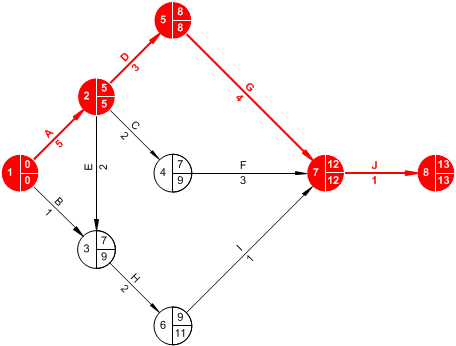
Gambar 6. Jalur Kritis dalam Activity Network Diagram
Gambar 6 di atas memperlihatkan node nomor 1, 2, 5, 7, dan 8 berada di jalur kritis. Selanjutnya perhatikan Tabel 2 di bawah ini yang memperlihatkan ES dan LS (Tabel 2.a) termasuk float time (Tabel 2.b) setiap kegiatan. Tampak kegiatan A, D, G, dan J berada di jalur kritis karena kegiatan-kegiatan tersebut tidak mempunyai waktu delay (perhatikan tanda cek pada Tabel 2.b).
Tabel 2
Tabel Analisis Jalur Kritis
(a) Perhitungan earliest start dan latest start time
| No. | Kegiatan (i, j) | Durasi,Dij | EET | LET | Earliest start time, ESij = Ei | Latest start time, LSij = Lj – Dij | ||
| Ei | Ej | Li | Lj | |||||
| 1 | A (1, 2) | 5 | 0 | 5 | 0 | 5 | 0 | 0 |
| 2 | B (1, 3) | 1 | 0 | 7 | 0 | 9 | 0 | 8 |
| 3 | C (2, 4) | 2 | 5 | 7 | 5 | 9 | 5 | 7 |
| 4 | D (2, 5) | 3 | 5 | 8 | 5 | 8 | 5 | 5 |
| 5 | E (2, 3) | 2 | 5 | 7 | 5 | 9 | 5 | 7 |
| 6 | F (4, 7) | 3 | 7 | 12 | 9 | 12 | 7 | 9 |
| 7 | G (5, 7) | 4 | 8 | 12 | 8 | 12 | 8 | 8 |
| 8 | H (3, 6) | 2 | 7 | 9 | 9 | 11 | 7 | 9 |
| 9 | I (6, 7) | 1 | 9 | 12 | 11 | 12 | 9 | 11 |
| 10 | J (7, 8) | 1 | 12 | 13 | 12 | 13 | 12 | 12 |
(b) Perhitungan activity float time
| No. | Kegiatan (i, j) | Durasi,Dij | EET | LET | Free float, FFij = Ej – Ei – Dij | Indp. float, IFij = Ej – Li – Dij | Total float, TFij = Lj – Ei – Dij | ||
| Ei | Ej | Li | Lj | ||||||
| 1 | A (1, 2) | 5 | 0 | 5 | 0 | 5 | 0 ✓ | 0 ✓ | 0 ✓ |
| 2 | B (1, 3) | 1 | 0 | 7 | 0 | 9 | 6 | 6 | 8 |
| 3 | C (2, 4) | 2 | 5 | 7 | 5 | 9 | 0 | 0 | 2 |
| 4 | D (2, 5) | 3 | 5 | 8 | 5 | 8 | 0 ✓ | 0 ✓ | 0 ✓ |
| 5 | E (2, 3) | 2 | 5 | 7 | 5 | 9 | 0 | 0 | 2 |
| 6 | F (4, 7) | 3 | 7 | 12 | 9 | 12 | 2 | 0 | 2 |
| 7 | G (5, 7) | 4 | 8 | 12 | 8 | 12 | 0 ✓ | 0 ✓ | 0 ✓ |
| 8 | H (3, 6) | 2 | 7 | 9 | 9 | 11 | 0 | 0 | 2 |
| 9 | I (6, 7) | 1 | 9 | 12 | 11 | 12 | 2 | 0 | 2 |
| 10 | J (7, 8) | 1 | 12 | 13 | 12 | 13 | 0 ✓ | 0 ✓ | 0 ✓ |
Activity network diagram yang erat kaitannya dengan metode CPM dan diagram PERT telah lama digunakan untuk tujuan memperlihatkan jalur penyelesaian suatu proyek, menemukan waktu penyelesaian proyek sesingkat mungkin, dan menggambarkan bagaimana kegiatan dapat serentak dilakukan dalam suatu proyek. Berikut hal-hal yang perlu diperhatikan dalam membuatactivity network diagram:
- Semua kegiatan dalam proyek, termasuk estimasi waktu yang dibutuhkan untuk setiap kegiatan, sebaiknya direncanakan dan dikomunikasikan bersama semua anggota team melalui mekanisme brainstorming. Estimasi waktu biasanya menggunakan pengalaman masa lalu atau perkiraan dari para praktisi.
- Kegiatan terurut dari awal sampai akhir, tidak boleh ada duplikasi kegiatan. Jika penambahan suatu kegiatan terjadi, kegiatan tambahan ini harus teridentifikasi dan digambarkan.
- Evaluasi kembali estimasi waktu terpendek, terpanjang, dan rata-rata untuk setiap kegiatan, dan identifikasi jalur terpanjang melalui jaringan.
- Gunakan diagram untuk melacak kemajuan atau progres setiap kegiatan. Pada saat proyek berlangsung, estimasi waktu dapat diperbarui sesuai dengan diperolehnya informasi dan asumsi baru. Tak hanya estimasi waktu, kita juga mungkin akan menemukan sebuah jalur kritis baru dan perubahan bentuk jaringan.
Rujukan:
Agustini, D. H., & Rahmadi, Y. E. (2004). Riset operasional: Konsep-konsep dasar. Jakarta: Rineka Cipta.
Baker, S. L. (2004). Critical path method (CPM). Retrieved fromhttp://hspm.sph.sc.edu/COURSES/J716/CPM/CPM.html
Hendrickson, C., & Tung, A. (2008). Project management for construction: Fundamental concepts for owners, engineers, architects and builders. (2.2 ed., chap. 10.3). Pittsburgh, PA: Prentice Hall. Retrieved fromhttp://pmbook.ce.cmu.edu/
Kelley Jr., J. E. (1961). Critical-path planning and scheduling: Mathematical basis. Operations Research, 9(3), 296–320. Retrieved fromhttp://or.journal.informs.org/content/9/3/296.full.pdf
Kusnadi, E. (2012, March 18). Activity network diagram: Bagian pertama [Web log post]. Retrieved fromhttps://eriskusnadi.wordpress.com/2012/03/18/activity-network-diagram-part-1/
Tague, N. R. (2005). The quality toolbox. (2th ed.). Milwaukee, Wisconsin: ASQ Quality Press. Available from http://asq.org/quality-press/display-item/index.html?item=H1224
Taylor, J. (2008). Project scheduling and cost control: Planning, monitoring and controlling the baseline. Ft. Lauderdale, Fla: J. Ross Pub.

